This post is also available in: English (Inglese)

Nel mondo dello sviluppo software l’analisi dei dati è sempre più centrale. Con l’avvento dell’intelligenza artificiale nel mercato consumer molti la utilizzano anche per analizzare dati statistici. In molti casi però l’uso di questa tecnologia non è richiesta ed è anzi meno efficiente di un solido algoritmo che si occupi di prendere dati in ingresso e restituire “black-box” dati in uscita.

L’intelligenza artificiale è ormai interpretata da molti imprenditori come una moda ma andrebbe utilizzata solo laddove è veramente un valore aggiunto. Parlando di efficienza, utilizzare l’intelligenza artificiale per calcolare una media, una mediana, una moda non è solamente come sparare con un bazooka per uccidere un paio di mosche ma può rivelarsi anche più lenta, dal momento che bisogna calcolare i tempi di inferenza, rispetto ad un algoritmo a stati finiti.

Anche in contesti non strettamente scientifici o accademici, conoscere i fondamenti della statistica descrittiva, può rivelarsi estremamente utile: dalla generazione di report automatizzati, al monitoraggio delle performance di un’applicazione, fino alla costruzione di dashboard o strumenti analitici.

In questo articolo realizzeremo una classe PHP che calcola i principali indicatori statistici descrittivi, come media, mediana, moda, varianza, deviazione standard, quartili, ecc., partendo da zero, senza librerie esterne. Il codice sarà pulito, riutilizzabile e pronto per essere trasfromato in un pacchetto Composer su cui verrà realizzato un altro articolo.

Progettare una classe semplice ma estensibile

Per costruire una classe di statistica descrittiva utile e facilmente integrabile in altri progetti, adotteremo una struttura ad oggetti aderente ai principi SOLID, evitando dipendenze esterne e garantendo la possibilità di estensoine futura (es. supporto a dataset associativi o lettura da file CSV).

La classe sarà progettata per lavorare su array di valori numerici, e calcolare in modo efficiente i principali indici statistici. L’obiettivo è offrire un’interfaccia semplice.

Per prima cosa andiamo a creare una nuova repo su GitHub, la trovate al link:
https://github.com/thesimon82/descriptive-statistics-php

Iniziamo ad implementare i metodi.

La struttura del progetto dovrà avere questa forma:

descriptive-statistics-php/
├─ composer.json
├─ composer.lock
├─ phpunit.xml
├─ examples/
│  └─ geometric_mean_demo.php
│  └─ harmonic_mean_demo.php
│  └─ iqr_demo.php
│  └─ mad_demo.php
│  └─ mean_demo.php
│  └─ median_demo.php
│  └─ min_max_demo.php
│  └─ mode_demo.php
│  └─ percentile_demo.php
│  └─ range_demo.php
│  └─ standard_deviation_demo.php
│  └─ trimmed_mean_demo.php
│  └─ variance_demo.php
├─ src/
│  └─ DescriptiveStats.php
├─ tests/
│  └─ DescriptiveStatsTest.php
└─ vendor/
    └─ autoload.php

Come puoi notare ho previsto anche una cartella per l’inserimento dei test sui metodi della classe (opzionale) con phpunit. Il file phpunit.xml definisce la cartella dei test ed i sorgenti di phpunit che deve essere installato tramite composer alla repo packagist phpunit/phpunit inserendolo come dipendenza di sviluppo tramite il comando composer require --dev phpunit/phpunit ^10.

Media

La media aritmetica (o valore medio) di un insieme di osservazioni numeriche si ottiene sommando tutti i valori e dividendo il risultato per il numero totale di osservazioni. Formalmente si scrive:

dove rappresenta la media aritmetica, è la cardinalità del campione e indica la somma di tutte le osservazioni. Questa misura fornisce un’indicazione sintetica della tendenza centrale dei dati, pur essendo sensibile alla presenza di valori anomali (outlier) che possono farla divergere significativamente dal “centro” reale della distribuzione.

Implementiamo questo metodo nella nostra classe DescriptiveStats.php

<?php

declare(strict_types=1);

namespace Renor\Statistics;

/**
 * Class DescriptiveStats
 *
 * A lightweight class to perform basic descriptive statistics on numeric datasets.
 */
class DescriptiveStats
{
    /**
     * @var float[] Filtered and normalized numeric dataset.
     */
    private array $data;

    /**
     * Main constructor.
     *
     * @param array $data An array containing the numeric values to be analyzed.
     * @throws \InvalidArgumentException If the array is empty or contains no numeric values.
     */
    public function __construct(array $data)
    {
        // Filter only numeric values (int or float) and reset array keys
        $filtered = array_filter($data, 'is_numeric');
        $this->data = array_values($filtered);

        if (count($this->data) === 0) {
            throw new \InvalidArgumentException('The dataset must contain at least one numeric value.');
        }
    }

    /**
     * Calculates the arithmetic mean of the dataset.
     *
     * @return float The arithmetic mean.
     */
    public function mean(): float
    {
        return array_sum($this->data) / count($this->data);
    }
}

Come puoi notare abbiamo dichiarato lo strict_types. Questa opzione impone a PHP di non effettuare il cast automatico del valori. Questo è necessario per avere il pieno controllo del tipo di dato.

Dal momento che accetteremo i dati come un array di valori dichiariamo una proprietà privata della classe private array $data.

Nel costruttore della classe ci occupiamo di recuperare i dati che vengono passati quando andremo ad istanziare la classe per creare un nuovo oggetto, verificando che il contenuto dell’array $data sia di tipo numerico, ed andiamo a posizionare i valori all’interno della proprietà $this->data.

Nel metodo mean() andiamo a implementare la formula matematica della media: sommiamo tutti gli elementi dell’array passato e dividiamo per il numero di elementi ritornando il risultato.

Mediana

La mediana rappresenta il valore centrale di un insieme ordinato di osservazioni e suddivide il campione in due metà di egual numerosità. Data una serie di valori tali che :

• Se è dispari, la mediana è semplicemente l’elemento in posizione :
  
• Se è pari, la mediana è la media aritmetica dei due elementi centrali:
  

A differenza della media aritmetica, la mediana è robusta rispetto agli outlier, poiché dipende solo dall’ordinamento dei dati e non dalla loro ampiezza.

 /**
     * Calculates the median (50th percentile) of the dataset.
     *
     * @return float The median value.
     */
    public function median(): float
    {
        // Clone and sort the dataset to avoid mutating the original array
        $sorted = $this->data;
        sort($sorted, SORT_NUMERIC);

        $count = count($sorted);
        $mid   = intdiv($count, 2);

        // If the count is odd, return the middle value
        if ($count % 2 === 1) {
            return (float) $sorted[$mid];
        }

        // If even, return the average of the two central values
        return ($sorted[$mid - 1] + $sorted[$mid]) / 2.0;
    }

In questo metodo recupero i dati e li ordino. Otteniamo la dimensione e ricarivamo l’indice centrale con la divisione intera. Ad esempio se abbiamo 7 elementi, intdiv(7,2) restituisce 3, che corrisponde alla quarta posizione (ricorda che gli array in PHP sono zero-based!). Se il numero di valori è dispari, esiste un unico elemento perfettamente centrale e lo restituisce. In caso di numerosità pari, invece non c’è un solo valore centrale, ce ne sono due, quello in posizione $mid - 1 e quello in posizione $mid. La mediana per definizione è la media aritmetica di questi due valori. Sommiamo quindi i centrali e dividiamo per 2.0 (con la notazione decimale per forzare la divisione in virgola mobile) ottenendo a sua volta un risultato float. In questo modo il metodo restituisce il cinquantesimo percentile del campione senza modificare il dataset originario e rispettando la definizione statistica sia per serie di lunghezza dispari che pari.

Moda

Dopo media e mediana, il terzo indicatore classicamente più utilizzato della statistica descrittiva è la moda, ossia il valore, o i valori, che ricorrono più spesso all’interno di un insieme di osservazioni. se denotiamo con la frequenza assoluta di un valore nel campione, la moda si ottiene come

.

Possiamo distinguere per la serie di valori in ingresso:

• Serie unimodale quando un solo valore ha la frequenza massima
• Serie multimodale quando due o più valori condividono la frequenza massima
• Serie senza moda quanto tutti i valori della serie compaiono all’interno della stessa una sola volta

La moda è particolarmente utile quando i dati sono categorici o quando si vuole evidenziare la concentrazione attorno a determinati valori interi. A differenza di media e mediana non misura la posizione centrale ma il valore o i valori che si ripetono maggiormente nella serie. Non a caso quando un capo d’abbigliamento è di moda è perché questo, rispetto ad altri capi d’abbigliamento in una serie di vendite, risulta quello più venduto e quindi “quello che va più di moda”.

Aggiungiamo quindi il metodo alla nostra classe:

/**
 * Returns the mode(s) of the dataset.
 *
 * If the dataset is multimodal, an array with all modal values is returned.
 * If every value occurs only once, an empty array is returned (no mode).
 *
 * @return float[] list of modal values
 */
public function mode(): array
{
    // Build a frequency table: value => occurrences
    $frequencies = array_count_values($this->data);

    // Determine the highest frequency
    $maxFrequency = max($frequencies);

    // If every value appears only once, there is no mode
    if ($maxFrequency === 1) {
        return [];
    }

    // Collect all values that share the highest frequency
    $modes = [];
    foreach ($frequencies as $value => $count) {
        if ($count === $maxFrequency) {
            // Cast to float so that return type is consistent
            $modes[] = (float) $value;
        }
    }

    sort($modes, SORT_NUMERIC); // return modes in ascending order
    return $modes;
}

array_count_values() scorre l’intero dataset e restituisce un array associativo in cui la chiave è il valore osservato e il valore è quante volte ricorre. È un modo rapido per calcolare per ogni .
Con max($frequencies) otteniamo il numero di occorrenze più alto presente nella tabella; è il valore di nella definizione matematica.
Se la frequenza massima è 1, significa che ogni osservazione è unica. In tal caso il metodo restituisce un array vuoto per indicare che non esiste alcun valore modale.
Si itera sulla tabella delle frequenze: per ogni chiave il cui conteggio eguaglia la frequenza massima, si aggiunge quel valore (cast a float) all’array $modes. In questo modo vengono inclusi tutti i valori modali in caso di multimodalità.
Prima di restituire il risultato, sort($modes, SORT_NUMERIC) assicura che le mode siano ordinate in senso crescente, rendendo più prevedibile l’output.

In questo modo abbiamo coperto tutti i possibili scenari: unimodali, multimodali e senza moda.

Media geometrica

La media geometrica è la misura di tendenza centrale più adatta quando i dati rappresentano tassi di crescita o rapporti (per esempio rendimenti percentuali, indici di variazione, scale logaritmiche).

Data una serie di valori tutti strettamente positivi , la media geometrica si definisce come:

oppure in forma logaritmica più stabile numericamente

.

Questa quantità corrisponde al fattore di crescita “medio” che, applicato n volte in sequenza, produce lo stesso risultato del prodotto reale dei valori.

/**
 * Calculates the geometric mean of the dataset.
 *
 * @throws \DomainException If any value is zero or negative.
 * @return float The geometric mean.
 */
public function geometricMean(): float
{
    // The geometric mean is defined only for strictly positive numbers.
    foreach ($this->data as $value) {
        if ($value <= 0) {
            throw new \DomainException('Geometric mean requires all values to be greater than zero.');
        }
    }

    // Use logarithms for numerical stability: exp( (1/n) * sum(log(x_i)) )
    $logSum = array_sum(array_map('log', $this->data));
    return exp($logSum / count($this->data));
}

Poiché la media geometrica è definita solo per numeri positivi, il metodo scorre il dataset e lancia una DomainException se trova valori ≤ 0. Questo previene risultati matematicamente scorretti (o complessi).
Invece di calcolare direttamente il prodotto (che potrebbe facilmente andare in overflow), convertiamo ogni valore con log(), sommiamo i logaritmi e dividiamo per . In base alle proprietà dei logaritmi:


Applicando exp() al valore medio dei logaritmi otteniamo la media geometrica.

Media armonica

La media armonica è la misura di tendenza centrale più indicata quando i dati rappresentano velocità, rapporti o frazioni: per esempio km / h percorsi a diversi ritmi, costo medio per unità o rendimento medio di investimenti calcolato come “quote per euro”.

Data una serie di valori positivi (nessun valore può essere zero, perché apparirebbe al denominatore), la media armonica si definisce come: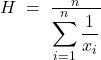

In altre parole si calcola l’inverso della media aritmetica degli inversi. Rispetto alla media aritmetica, la media armonica pesa di più i valori piccoli: è quindi preziosa quando si desidera penalizzare fortemente le prestazioni peggiori (es.: il tempo medio per percorrere un chilometro su più tratte di diversa velocità).

/**
 * Calculates the harmonic mean of the dataset.
 *
 * @throws \DomainException If any value is zero or negative.
 * @return float The harmonic mean.
 */
public function harmonicMean(): float
{
    // Harmonic mean is defined only for strictly positive numbers.
    foreach ($this->data as $value) {
        if ($value <= 0) {
            throw new \DomainException('Harmonic mean requires all values to be greater than zero.');
        }
    }

    $inverseSum = array_sum(array_map(
        static fn (float $v): float => 1.0 / $v,
        $this->data
    ));

    return count($this->data) / $inverseSum;
}

Per prima cosa si effettua un controllo di dominio, qualunque valore maggiore o uguale a zero genera una DomainException, altrimenti il risultato non sarebbe definitivo o diverrebbe infinito. Poi si effettua una somma degli inversi: array_map() calcola l’inverso di ogni elemento, array_sum() li somma.
La formula diretta divide il numero di osservazioni per la somma ottenuta, secondo la definizione matematica.

Troncamento della media (o media troncata)

Quando un campione contiene outlier estremi che rischiano di distorcere la media aritmetica, una soluzione elegante è la media troncata (o trimmed mean).

Si sceglie una percentuale % (tipicamente 5 % oppure 10 %), si ordina il campione e si scartano le prime osservazioni più piccole e le ultime più grandi, dove

.

In questo modo si ottiene una misura di tendenza centrale più robusta della media aritmetica ma meno drastica della mediana.

/**
 * Calculates the trimmed mean of the dataset.
 *
 * @param float $percent Percentage (0–50) of data to trim at each tail.
 * @throws \DomainException If $percent is out of range or removes all data.
 * @return float The trimmed mean.
 */
public function trimmedMean(float $percent): float
{
    if ($percent < 0.0 || $percent >= 50.0) {
        throw new \DomainException('Percent must be in the range 0 <= p < 50.');
    }

    $count = count($this->data);
    if ($count < 3) {
        // Too few values to trim meaningfully; fall back to arithmetic mean
        return $this->mean();
    }

    // Clone and sort to preserve original order
    $sorted = $this->data;
    sort($sorted, SORT_NUMERIC);

    // Number of elements to trim from each end
    $k = (int) floor($count * $percent / 100.0);

    // Ensure at least one value remains
    if ($k * 2 >= $count) {
        throw new \DomainException('Trim percentage removes all data.');
    }

    $trimmed = array_slice($sorted, $k, $count - 2 * $k);

    return array_sum($trimmed) / count($trimmed);
}

Il metodo inizia verificando che la percentuale scelta per il taglio sia sensata: deve essere maggiore o uguale a zero e strettamente minore di cinquanta, altrimenti si solleva un’eccezione; se chiedessimo, ad esempio, di eliminare il 60 % di dati a ciascuna coda non rimarrebbe nulla da mediare.

Se il campione contiene meno di tre osservazioni, la funzione considera il taglio privo di significato e restituisce semplicemente la media aritmetica: con due valori, infatti eliminare anche solo un elemento farebbe sparire metà dei dati, mentre con uno solo non esiste nulla da troncare.

Si procede poi a clonare l’array originale e a ordinarlo in senso crescente; la clonazione preserva l’ordine in cui i dati erano stati forniti all’oggetto, mentre l’ordinamento è indispensabile perché il troncamento viene applicato partendo dagli estremi della distribuzione.

Il numero di elementi da scartare in ciascuna coda, indicato con , si ottiene moltiplicando la dimensione del campione per la percentuale richiesta e arrotondando verso il basso; se ad esempio abbiamo dieci valori e vogliamo una trimmed mean al 10 %, toglieremo un elemento all’inizio e uno alla fine.

Prima di procedere, il metodo controlla che ‟due volte ” non sia pari o superiore alla lunghezza dell’array: se così fosse, il taglio eliminerebbe tutti i dati e la media non avrebbe più senso; in tal caso viene lanciata un’ulteriore eccezione.

Superata questa verifica, array_slice() preleva la porzione centrale che rimane dopo aver scartato i valori minori e i maggiori; su tale sottoinsieme si calcola infine la media aritmetica, che è proprio la media troncata desiderata.

La funzione restituisce così un indicatore di tendenza centrale più robusto della media classica: gli outlier, rimossi prima del calcolo, non possono più trascinare il risultato verso valori estremi.

Range

Il range è la misura di dispersione più semplice: indica l’ampiezza totale dei valori osservati, ossia la distanza fra l’estremo minimo e quello massimo del campione. Se chiamiamo

,

allora il range si definisce come

.

Pur essendo sensibile agli outlier (lo stesso valore che condiziona il massimo o il minimo condiziona anche il range), questa misura offre un’indicazione immediata della larghezza della distribuzione e viene spesso riportata accanto a medie o mediana per dare un colpo d’occhio sulla dispersione complessiva.

/**
 * Calculates the range (max – min) of the dataset.
 *
 * @return float The range of the data.
 */
public function range(): float
{
    // min() e max() sono O(n) ma il dataset è già in memoria: soluzione lineare
    return max($this->data) - min($this->data);
}

Il metodo come è possibile vedere è molto essenziale. Si invocano le funzioni PHP native max() e min()che eseguono una sola scansione lineare dell’array per individuare rispettivamente il valore più grande e quello più piccolo. Sottraendo il minimo dal massimo si ottiene l’ampiezza totale del campione; il risultato è restituito come float, coerente con gli altri metodi della classe.

Quartili e intervallo quartile (IQR)

Per descrivere la dispersione di un campione in modo più robusto rispetto al semplice range, si ricorre ai quartili:

• – 25° percentile (primo quartile)
• – 50° percentile (mediana)
• – 75° percentile (terzo quartile)

L’intervallo interquartile si definisce come e rappresenta l’ampiezza della metà centrale dei dati. È poco sensibile agli outlier perché si basa solo sui valori compresi fra il 25% e il 75% della distribuzione.

Un uso classico dell’IQR è il rilevamento degli outlier col metodo di Tukey  (valori minori di o maggiori di )

/**
 * Returns an array with the first, second (median) and third quartile.
 *
 * Method: "Tukey hinges".
 *  - Sort the dataset.
 *  - For Q1 and Q3, exclude the median when the sample size is odd.
 *
 * @return float[] [Q1, Q2, Q3] in ascending order.
 */
 public function quartiles(): array
    {
        $sorted = $this->data;
        sort($sorted, SORT_NUMERIC);

        $n = count($sorted);
        if ($n === 1) {
            return [$sorted[0], $sorted[0], $sorted[0]];
        }
        $mid = intdiv($n, 2);

        // Median (Q2)
        $q2 = ($n % 2 === 0)
            ? ($sorted[$mid - 1] + $sorted[$mid]) / 2.0
            : (float) $sorted[$mid];

        // Lower half (exclude median if n is odd)
        $lower = array_slice($sorted, 0, $mid);
        // Upper half (exclude median if n is odd)
        $upper = array_slice($sorted, ($n % 2 === 0) ? $mid : $mid + 1);

        // Q1 and Q3 are medians of the two halves
        $q1 = $this->medianOfArray($lower);
        $q3 = $this->medianOfArray($upper);

        return [$q1, $q2, $q3];
    }

/**
 * Calculates the interquartile range (Q3 – Q1).
 *
 * @return float The interquartile range.
 */
public function iqr(): float
{
    [$q1, , $q3] = $this->quartiles();
    return $q3 - $q1;
}

/* ---------- Helper ---------- */
/**
 * Median of a pre-sorted array (helper for quartiles).
 *
 * @param float[] $arr Sorted numeric array.
 * @return float Median value.
 */
private function medianOfArray(array $arr): float
{
    $count = count($arr);
    if ($count === 0) {
        throw new \LogicException('Cannot compute median of an empty array.');
    }

    $mid = intdiv($count, 2);

    return ($count % 2 === 0)
        ? ($arr[$mid - 1] + $arr[$mid]) / 2.0
        : (float) $arr[$mid];
}

Quando il metodo quartiles() viene invocato, la prima cosa che fa è creare una copia dei dati interni e ordinarla in senso crescente; questa copia protegge l’ordine originale fornito dall’utente e consente di lavorare con un vettore monotonicamente ordinato, prerequisito indispensabile per individuare i quartili. Subito dopo, la variabile $n memorizza la lunghezza del campione e $mid rappresenta l’indice centrale calcolato tramite divisione intera. Con queste due informazioni si procede a determinare la mediana dell’intero campione, che diventa il secondo quartile ; se il numero di osservazioni è pari, la mediana è la media aritmetica dei due valori centrali, mentre nel caso dispari coincide con il valore in posizione centrale.

Una volta noto , l’array ordinato viene spezzato in due metà. Se la numerosità è dispari la mediana non va inclusa né nella parte inferiore né in quella superiore, perciò la funzione array_slice la esclude esplicitamente; se è pari la suddivisione avviene esattamente a metà. A questo punto entrano in gioco i quartili estremi: per calcolare e non si crea alcun nuovo oggetto, bensì si invoca l’helper privato medianOfArray sulle due metà già ordinate. Questa piccola routine riceve un vettore, ne conta gli elementi, determina l’indice centrale e restituisce la mediana con la stessa logica adottata in precedenza; il tutto resta confinato all’interno della classe, così l’interfaccia pubblica rimane pulita e ogni duplicazione di codice è evitata.

Il metodo quartiles() restituisce infine un array con i tre valori in ordine crescente. Il fratello iqr() si limita a scompattare quell’array, sottrae da e ritorna l’intervallo interquartile, fornendo in un’unica chiamata la misura di dispersione più robusta della classe.

In questo assetto la logica della mediana resta centralizzata dentro l’helper privato, viene riutilizzata sia per i quartili sia, in modo implicito, per qualsiasi eventuale altra funzionalità interna che avesse bisogno di calcolare una mediana su un sottoinsieme ordinato, mentre l’API pubblica continua ad offrire metodi autodidattici e facili da comprendere per chi integrerà la tua libreria.

Varianza

Per misurare quanto i valori si discostino dalla loro tendenza centrale si introduce la varianza, che calcola la media dei quadrati degli scarti dalla media aritmetica. Date osservazioni con media , la varianza della popolazione si definisce

Se invece i dati rappresentano un campione estratto da una popolazione più ampia, lo stimatore corretto (varianza campionaria) divide per :

La varianza restituisce un valore quadratico: è sempre non negativa e cresce rapidamente quando gli scarti aumentano, perciò un suo uso frequente è passare alla radice quadrata (deviazione standard) per tornare alle stesse unità di misura dei dati.

/**
 * Calculates the variance of the dataset.
 *
 * @param bool $sample If true, uses (n-1) in the denominator (sample variance).
 *                     If false, uses n (population variance).
 * @return float The variance value.
 */
public function variance(bool $sample = false): float
{
    $n = count($this->data);

    // For a single value, population variance is 0, sample variance is undefined
    if ($n < 2 && $sample) {
        throw new \DomainException('Sample variance requires at least two observations.');
    }
    if ($n === 1) {
        return 0.0;
    }

    $mean = $this->mean();
    $sumSquares = 0.0;

    foreach ($this->data as $v) {
        $diff        = $v - $mean;
        $sumSquares += $diff * $diff;
    }

    $denominator = $sample ? ($n - 1) : $n;
    return $sumSquares / $denominator;
}

Il metodo riceve un flag che indica se calcolare la varianza della popolazione o lo stimatore campionario. Inizia valutando la numerosità del dataset: con un solo valore la varianza di popolazione è per definizione zero, mentre quella campionaria non esiste e viene sollevata un’eccezione. Una volta nota la media, il ciclo attraversa ogni osservazione, sottrae la media, eleva lo scarto al quadrato e lo accumula. Terminata la sommatoria, la divisione avviene per o a seconda del contesto specificato, restituendo così la misura di dispersione desiderata.

Deviazione standard

La deviazione standard non è altro che la radice quadrata della varianza: serve a riportare la misura di dispersione alle stesse unità dei dati originali. Se la varianza indica “quanti quadrati di unità” si distanziano in media le osservazioni dalla loro media, la deviazione standard esprime quello scarto in unità lineari, dunque risulta molto più intuitiva per un lettore non specialista. Per la popolazione la si ottiene come , mentre nel caso campionario si usa . Valori di deviazione standard piccoli raccontano una distribuzione raccolta intorno alla media; valori grandi parlano di dati molto dispersi.

/**
 * Calculates the standard deviation of the dataset.
 *
 * @param bool $sample If true, returns the sample standard deviation (n-1 in the denominator).
 *                     If false, returns the population standard deviation.
 * @return float The standard deviation.
 */
public function standardDeviation(bool $sample = false): float
{
    return sqrt($this->variance($sample));
}

Il metodo non contiene logica aggiuntiva: richiama semplicemente variance() con lo stesso flag e ne restituisce la radice quadrata, delegando all’algoritmo già collaudato tutta la parte di calcolo e di controlli di dominio.

Errore standard della media

Quando dalla popolazione osserviamo soltanto un campione, la media campionaria è una stima soggetta a fluttuazioni: più il campione è piccolo, più la stima può variare da un campione all’altro. L’errore standard della media (in inglese Standard Error of the Mean, SEM) quantifica esattamente questa variabilità prevista. Se s è la deviazione standard campionaria e n è la numerosità del campione, l’errore standard si calcola con

.

Un SEM contenuto indica che la media calcolata su quel campione è verosimilmente vicina alla media vera della popolazione; un SEM ampio suggerisce un’incertezza maggiore. Il SEM è inoltre la base per costruire gli intervalli di confidenza della media.

/**
 * Calculates the standard error of the mean (SEM) of the dataset.
 *
 * SEM = sample standard deviation / sqrt(n)
 * Requires at least two observations.
 *
 * @throws \DomainException If the dataset size is less than 2.
 * @return float The standard error of the mean.
 */
public function standardError(): float
{
    $n = count($this->data);

    if ($n < 2) {
        throw new \DomainException('Standard error requires at least two observations.');
    }

    return $this->standardDeviation(true) / sqrt($n);
}

Il metodo prende innanzitutto la dimensione del campione; se c’è un solo valore non ha senso parlare di errore standard, perciò viene sollevata un’eccezione di dominio. In tutti gli altri casi richiama la deviazione standard campionaria già implementata, ottenendo . Dividendo per la radice quadrata di n ricava il SEM secondo la definizione statistica canonica e restituisce il risultato come valore in virgola mobile. In questo modo tutta la logica numerica rimane coerente con le altre misure di dispersione: la funzione si appoggia a metodi collaudati, non replica calcoli già presenti e garantisce un contratto d’uso molto semplice.

Scarto assoluto medio

Per misurare la dispersione in modo intuitivo, senza amplificare gli scarti con il quadrato come fa la varianza, si utilizza lo scarto assoluto medio. L’idea è semplice: si calcola la distanza assoluta fra ogni osservazione e la media aritmetica, poi si fa la media di quelle distanze. Se il campione è composto dai valori e la loro media è , lo scarto assoluto medio si ottiene con

.

Lo scarto assoluto medio mantiene le stesse unità di misura dei dati, è meno sensibile agli outlier rispetto alla deviazione standard e offre un’interpretazione immediata: indica di quante unità, in media, ogni valore si discosta dal centro della distribuzione.

/**
 * Calculates the mean absolute deviation (MAD) of the dataset.
 *
 * @return float The mean absolute deviation.
 */
public function meanAbsoluteDeviation(): float
{
    $mean = $this->mean();
    $sumAbs = 0.0;

    foreach ($this->data as $v) {
        $sumAbs += abs($v - $mean);
    }

    return $sumAbs / count($this->data);
}

Il metodo ricava innanzitutto la media aritmetica del campione tramite la funzione già esistente mean(). Con questa informazione scorre ogni osservazione, sottrae la media, prende il valore assoluto dello scarto e lo accumula in $sumAbs. Una volta terminato il ciclo divide la somma degli scarti assoluti per la numerosità del campione, restituendo il risultato in virgola mobile. La logica rimane lineare e senza rami condizionali perché la formula del MAD non richiede distinzioni tra popolazione e campione: vale sempre la divisione per .

Percentili

Per localizzare un valore qualsiasi lungo la distribuzione si utilizzano i percentili: il percentile individua il punto sotto il quale ricade esattamente la percentuale dei dati ordinati. Il 50° percentile coincide con la mediana, il 25° e il 75° formano i quartili già implementati e, in generale, conoscere più percentili permette di descrivere la forma della distribuzione in maniera molto dettagliata. Poiché il campione è finito, la posizione del percentile raramente coincide con un indice intero: occorre dunque interpolare fra gli elementi adiacenti. Una convenzione ampiamente adottata (Excel e NumPy “linear” method) consiste nel calcolare

dove è la numerosità: se r cade fra gli indici e , il percentile è la combinazione lineare dei due valori con peso uguale alla parte frazionaria di .

/**
 * Returns the p-th percentile of the dataset (linear interpolation).
 *
 * @param float $p Percentile in the closed range [0, 100].
 * @throws \DomainException If $p is outside 0–100.
 * @return float The requested percentile.
 */
public function percentile(float $p): float
{
    if ($p < 0.0 || $p > 100.0) {
        throw new \DomainException('Percentile must be between 0 and 100.');
    }

    $sorted = $this->data;
    sort($sorted, SORT_NUMERIC);
    $n = count($sorted);

    // Edge cases: 0th and 100th percentile
    if ($p === 0.0)   { return (float) $sorted[0]; }
    if ($p === 100.0) { return (float) $sorted[$n - 1]; }

    // Linear-interpolated rank
    $rank        = ($p / 100.0) * ($n - 1);
    $lowerIndex  = (int) floor($rank);
    $upperIndex  = (int) ceil($rank);
    $weightUpper = $rank - $lowerIndex;

    // If rank is an integer, no interpolation is needed
    if ($lowerIndex === $upperIndex) {
        return (float) $sorted[$lowerIndex];
    }

    $lowerValue = $sorted[$lowerIndex];
    $upperValue = $sorted[$upperIndex];

    return (1.0 - $weightUpper) * $lowerValue + $weightUpper * $upperValue;
}

Il metodo convalida innanzitutto che il percentile richiesto sia compreso fra 0 e 100 inclusi, garantendo così coerenza con la definizione statistica. Subito dopo crea una copia ordinata dei dati, perché qualsiasi localizzazione percentuale richiede il vettore monotònicamente crescente. Gli estremi 0 e 100 vengono gestiti esplicitamente restituendo rispettivamente il minimo e il massimo del campione. Per tutti gli altri valori si calcola il rango reale , che può cadere fra due indici interi; l’indice inferiore e quello superiore delimitano l’intervallo che contiene la posizione frazionaria. Se è già intero non serve interpolazione e il metodo restituisce direttamente l’elemento corrispondente. In caso contrario si combinano linearmente il valore inferiore e quello superiore con un peso uguale alla parte decimale di , producendo un risultato continuo che scorre uniformemente fra gli elementi del campione.

Minimo e Massimo

Per completare il quadro delle misure descrittive è utile poter recuperare rapidamente l’estremo inferiore e quello superiore della distribuzione. Il valore minimo indica l’osservazione più piccola registrata nel campione; il valore massimo segnala la più grande. Queste due grandezze, pur estremamente semplici, sono indispensabili sia per dare il contesto ai dati (sapere dove inizia e dove finisce l’intervallo effettivamente osservato) sia come ingrediente di altre statistiche, ad esempio il range che hai già implementato. Poiché il dataset è interamente in memoria, individuare minimo e massimo richiede una sola scansione lineare e il costo computazionale è trascurabile.

/**
 * Returns the minimum value of the dataset.
 *
 * @return float The smallest observation.
 */
public function minValue(): float
{
    return (float) min($this->data);
}

/**
 * Returns the maximum value of the dataset.
 *
 * @return float The largest observation.
 */
public function maxValue(): float
{
    return (float) max($this->data);
}

Le funzioni PHP min() e max() attraversano l’array una sola volta; il cast garantisce che il tipo restituito sia float, uniforme con il resto dell’API.

Conclusioni

Con questo ultimo metodo abbiamo completato la nostra Classe DescriptiveStats che ora racchiude in un unico componente i più importanti strumenti di statistica descrittiva: dalle misure di posizione (media aritmetica, mediana, moda, percentili) alle misure di dispersione (range, varianza, deviazione standard, IQR, MAD), passando per indicatori di robustezza (media troncata) e incertezza (errore standard). Ogni funzione è autonoma, tipizzata e corredata di test automatici con PHPUnit che non abbiamo riportato per non allungare ulteriormente questo articolo già abbastanza pregno di nozioni.

Grazie a questa libreria, un progetto PHP può analizzare rapidamente piccoli dataset senza dipendenze esterne e senza dover utilizzare l’intelligenza artificiale solo per “moda”, integrare calcoli statistici in report, dashboard o API, estendere la classe con ulteriori indicatori sfruttando un’architettura chiara e coerente.

Nel prossimo articolo vedremo come trasformare il codice in un pacchetto Composer: creeremo la struttura definitiva della repository, vedremo come modificare il file composer.json, configureremo la CI per eseguire i test e pubblicheremo la libreria su Packagist, rendendola installabile con un semplice:

composer require thesimon82/descriptive-statistics

In questo modo potrai distribuire la tua soluzione open-source, ricevere contributi dalla community e riutilizzarla in qualsiasi progetto con la massima semplicità.

• About
• Latest Posts

Seguimi

Simone Renzi

CEO at RENOR & Partners

Senior full-stack web engineer, con oltre 15 anni di esperienza in architetture cloud, AI e soluzioni SaaS; socio di Mensa Italia. Ideatore di piattaforme come HR24.ai e Paghe.ai, ha curato lo sviluppo web di FNS, simulatore di reti neurali citato su Scientific Reports (Nature Portfolio), ed ha collaborato a progetti di ricerca con INFN – Laboratori Nazionali di Frascati, Università di Roma “Tor Vergata”, Universidad Complutense, Universidad Politécnica e Centro de Tecnología Biomédica di Madrid. Pianista classico, fonde creatività musicale e rigore tecnologico in ogni progetto.

Seguimi

Latest posts by Simone Renzi (see all)

• L’AI che sa tutto di te - Maggio 30, 2025
• L’importanza di fidarsi dei propri collaboratori - Maggio 26, 2025
• SpectraScan Gluten: il rilevatore tascabile di glutine per celiaci - Maggio 25, 2025