Sei interessato ai nostri servizi di consulenza?

1 Clicca nella sezione contatti
2 Compila il form
3 Ti ricontattiamo

Se hai bisogno urgente del nostro intervento puoi contattarci al numero 370 148 9430

RENOR & Partners

I nostri orari
Lun-Ven 9:00AM - 18:PM
May 12, 2025

A Descriptive Statistics Class in PHP

A Descriptive Statistics Class in PHP

by Simone Renzi / May 12, 2025
Post Image

This post is also available in: Italiano (Italian)

In the world of software development, data analysis is becoming increasingly central. With the advent of artificial intelligence in the consumer market, many now use it to analyze statistical data as well. However, in many cases, the use of this technology is not required and is actually less efficient than a solid algorithm designed to take input data and return output data in a “black-box” manner.

Artificial intelligence is now seen by many entrepreneurs as a trend, but it should only be used where it truly adds value. Speaking of efficiency, using AI to calculate a mean, a median, or a mode is not only like using a bazooka to kill a couple of flies, but it can also turn out to be slower, considering the inference times, compared to a finite state algorithm.

Even in contexts that are not strictly scientific or academic, knowing the fundamentals of descriptive statistics can prove extremely useful: from generating automated reports, to monitoring an application’s performance, and even to building dashboards or analytical tools.

In this article, we will build a PHP class that calculates the main descriptive statistical indicators—such as mean, median, mode, variance, standard deviation, quartiles, and more—from scratch, without relying on external libraries. The code will be clean, reusable, and ready to be transformed into a Composer package, which will be the subject of a follow-up article.

Designing a simple yet extensible class

To build a useful and easily integrable descriptive statistics class, we will adopt an object-oriented structure aligned with SOLID principles, avoiding external dependencies and ensuring the possibility of future extension (e.g., support for associative datasets or reading from CSV files).

The class will be designed to operate on arrays of numerical values and efficiently compute the main statistical indicators. The goal is to provide a simple interface.

First, let’s create a new repository on GitHub, which you can find at the following link:
https://github.com/thesimon82/descriptive-statistics-php

Let’s start implementing the methods.

The project structure should be as follows: 

descriptive-statistics-php/
├─ composer.json
├─ composer.lock
├─ phpunit.xml
├─ examples/
│  └─ geometric_mean_demo.php
│  └─ harmonic_mean_demo.php
│  └─ iqr_demo.php
│  └─ mad_demo.php
│  └─ mean_demo.php
│  └─ median_demo.php
│  └─ min_max_demo.php
│  └─ mode_demo.php
│  └─ percentile_demo.php
│  └─ range_demo.php
│  └─ standard_deviation_demo.php
│  └─ trimmed_mean_demo.php
│  └─ variance_demo.php
├─ src/
│  └─ DescriptiveStats.php
├─ tests/
│  └─ DescriptiveStatsTest.php
└─ vendor/
    └─ autoload.php

As you can see, I have also included a folder for adding tests on the class methods (optional) using PHPUnit. The phpunit.xml file defines the test folder and the PHPUnit sources, which must be installed via Composer from the Packagist repository phpunit/phpunit, adding it as a development dependency using the command composer require --dev phpunit/phpunit ^10.

Mean

The arithmetic mean (or average) of a set of n numerical observations x_1, x_2, \dots, x_n is obtained by summing all the values and dividing the result by the total number of observations. Formally, it is written as:


\bar{x} \;=\; \frac{1}{n} \sum_{i=1}^{n} x_i


where \bar{x} represents the arithmetic mean, n is the sample size, and \sum_{i=1}^{n} x_i indicates the sum of all observations. This measure provides a concise indication of the central tendency of the data, although it is sensitive to the presence of outliers, which can cause it to deviate significantly from the actual “center” of the distribution.

Let’s implement this method in our class. DescriptiveStats.php

<?php

declare(strict_types=1);

namespace Renor\Statistics;

/**
 * Class DescriptiveStats
 *
 * A lightweight class to perform basic descriptive statistics on numeric datasets.
 */
class DescriptiveStats
{
    /**
     * @var float[] Filtered and normalized numeric dataset.
     */
    private array $data;

    /**
     * Main constructor.
     *
     * @param array $data An array containing the numeric values to be analyzed.
     * @throws \InvalidArgumentException If the array is empty or contains no numeric values.
     */
    public function __construct(array $data)
    {
        // Filter only numeric values (int or float) and reset array keys
        $filtered = array_filter($data, 'is_numeric');
        $this->data = array_values($filtered);

        if (count($this->data) === 0) {
            throw new \InvalidArgumentException('The dataset must contain at least one numeric value.');
        }
    }

    /**
     * Calculates the arithmetic mean of the dataset.
     *
     * @return float The arithmetic mean.
     */
    public function mean(): float
    {
        return array_sum($this->data) / count($this->data);
    }
}

As you can see, we have declared strict_types. This directive enforces PHP to avoid automatic type coercion, which is essential when we want full control over data types.

Since we will accept the data as an array of values, we declare a private property of the class private array $data.

In the class constructor, we handle retrieving the data passed when instantiating the class to create a new object, verifying that the contents of the array $data are numeric, and we place the values inside the property $this->data.

In the mean() method, we implement the mathematical formula for the mean: we sum all the elements of the passed array and divide by the number of elements, returning the result.

Median

The median represents the central value of an ordered set of observations and divides the sample into two halves of equal size. Given a series of n values x_1, x_2, \dots, x_n such that x_1 \le x_2 \le \dots \le x_n:

  • If n is odd, the median is simply the element in position \frac{n+1}{2}:
    \text{Mediana} = x_{\frac{n+1}{2}}
  • If n is even, the median is the arithmetic mean of the two central elements:
    \text{Mediana} = \frac{x_{\frac{n}{2}} + x_{\frac{n}{2}+1}}{2}

Unlike the arithmetic mean, the median is robust to outliers, as it depends only on the ordering of the data and not on their magnitude. 

 /**
     * Calculates the median (50th percentile) of the dataset.
     *
     * @return float The median value.
     */
    public function median(): float
    {
        // Clone and sort the dataset to avoid mutating the original array
        $sorted = $this->data;
        sort($sorted, SORT_NUMERIC);

        $count = count($sorted);
        $mid   = intdiv($count, 2);

        // If the count is odd, return the middle value
        if ($count % 2 === 1) {
            return (float) $sorted[$mid];
        }

        // If even, return the average of the two central values
        return ($sorted[$mid - 1] + $sorted[$mid]) / 2.0;
    }

In this method, I retrieve the data and sort it. We get the size and calculate the central index using integer division. For example, if we have 7 elements, intdiv(7,2) returns 3, which corresponds to the fourth position (remember that arrays in PHP are zero-based!). If the number of values is odd, there is a single perfectly central element, and it is returned. In the case of an even number of values, however, there is not just one central value but two: the ones in positions $mid - 1 and $mid. By definition, the median is the arithmetic mean of these two values. We therefore sum the central elements and divide by 2.0 (using decimal notation to force floating-point division), which returns a float result. This way, the method returns the fiftieth percentile of the sample without modifying the original dataset and in accordance with the statistical definition for both odd and even-length series.

Mode

After the mean and the median, the third most commonly used indicator in descriptive statistics is the mode, that is, the value or values that occur most frequently within a set of observations. If we denote by f(x) the absolute frequency of a value x in the sample, the mode is obtained as:

\text{Moda} = \operatorname*{arg\,max}_{x}\; f(x).

We can distinguish, based on the input data series:

  • Unimodal series when only one value has the highest frequency
  • Multimodal series when two or more values share the highest frequency
  • Series without a mode when all the values in the series appear only once each

The mode is particularly useful when the data are categorical or when one wants to highlight concentration around certain integer values. Unlike the mean and the median, it does not measure central tendency but rather the value or values that occur most frequently in the series. It is no coincidence that when a clothing item is “in fashion” it is because, compared to other items in a sales series, it turns out to be the most sold and therefore “the one most in fashion.”

Let’s therefore add the method to our class:

/**
 * Returns the mode(s) of the dataset.
 *
 * If the dataset is multimodal, an array with all modal values is returned.
 * If every value occurs only once, an empty array is returned (no mode).
 *
 * @return float[] list of modal values
 */
public function mode(): array
{
    // Build a frequency table: value => occurrences
    $frequencies = array_count_values($this->data);

    // Determine the highest frequency
    $maxFrequency = max($frequencies);

    // If every value appears only once, there is no mode
    if ($maxFrequency === 1) {
        return [];
    }

    // Collect all values that share the highest frequency
    $modes = [];
    foreach ($frequencies as $value => $count) {
        if ($count === $maxFrequency) {
            // Cast to float so that return type is consistent
            $modes[] = (float) $value;
        }
    }

    sort($modes, SORT_NUMERIC); // return modes in ascending order
    return $modes;
}



array_count_values() It scans the entire dataset and returns an associative array where the key is the observed value and the value is the number of times it occurs. This is a quick way to calculate f(x) for each x.
With max($frequencies), we obtain the highest number of occurrences present in the table; this corresponds to the value of \max f(x) in the mathematical definition.
If the maximum frequency is 1, it means that each observation is unique. In this case, the method returns an empty array to indicate that no modal value exists.
We iterate over the frequency table: for each key whose count equals the maximum frequency, we add that value (cast to float) to the array $modes. In this way, all modal values are included in the case of multimodality.
Before returning the result, sort($modes, SORT_NUMERIC) ensures that the modes are sorted in ascending order, making the output more predictable.

In this way, we have covered all possible scenarios: unimodal, multimodal, and without a mode.

Geometric mean

The geometric mean is the most appropriate measure of central tendency when the data represent growth rates or ratios (for example, percentage returns, variation indices, logarithmic scales).

Given a series of n strictly positive values x_1, x_2, \dots, x_n, the geometric mean G is defined as:


G \;=\; \Bigl( \prod_{i=1}^{n} x_i \Bigr)^{\frac{1}{n}}

or, in a numerically more stable logarithmic form:

\ln G \;=\; \frac{1}{n} \sum_{i=1}^{n} \ln x_i.


This quantity corresponds to the “average” growth factor which, applied n times in sequence, yields the same result as the actual product of the values.

/**
 * Calculates the geometric mean of the dataset.
 *
 * @throws \DomainException If any value is zero or negative.
 * @return float The geometric mean.
 */
public function geometricMean(): float
{
    // The geometric mean is defined only for strictly positive numbers.
    foreach ($this->data as $value) {
        if ($value <= 0) {
            throw new \DomainException('Geometric mean requires all values to be greater than zero.');
        }
    }

    // Use logarithms for numerical stability: exp( (1/n) * sum(log(x_i)) )
    $logSum = array_sum(array_map('log', $this->data));
    return exp($logSum / count($this->data));
}



Since the geometric mean is only defined for positive numbers, the method scans the dataset and throws a DomainException if it encounters values ≤ 0. This prevents mathematically incorrect (or complex) results.
Instead of directly calculating the product (which could easily overflow), we convert each value using log(), sum the logarithms, and divide by n. Based on the properties of logarithms:
\ln\!\Bigl(\prod x_i\Bigr) \;=\; \sum \ln x_i

By applying exp() to the average of the logarithms, we obtain the geometric mean.
G \;=\; \exp\!\Bigl(\tfrac{1}{n}\sum \ln x_i\Bigr)

Harmonic mean

The harmonic mean is the most appropriate measure of central tendency when the data represent speeds, ratios, or fractions—for example, kilometers per hour traveled at different paces, average cost per unit, or average return on investments calculated as “units per euro.”

Given a series of n positive values x_1, x_2, \dots, x_n (no value can be zero, as it would appear in the denominator), the harmonic mean H is defined as:

H \;=\; \frac{n}{\displaystyle\sum_{i=1}^{n} \frac{1}{x_i}}

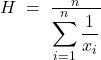
In other words, it is calculated as the inverse of the arithmetic mean of the reciprocals. Compared to the arithmetic mean, the harmonic mean gives more weight to smaller values: it is therefore valuable when one wishes to strongly penalize poorer performances (e.g., the average time to travel one kilometer over multiple segments at different speeds). 

/**
 * Calculates the harmonic mean of the dataset.
 *
 * @throws \DomainException If any value is zero or negative.
 * @return float The harmonic mean.
 */
public function harmonicMean(): float
{
    // Harmonic mean is defined only for strictly positive numbers.
    foreach ($this->data as $value) {
        if ($value <= 0) {
            throw new \DomainException('Harmonic mean requires all values to be greater than zero.');
        }
    }

    $inverseSum = array_sum(array_map(
        static fn (float $v): float => 1.0 / $v,
        $this->data
    ));

    return count($this->data) / $inverseSum;
}

First, a domain check is performed: any value less than or equal to zero triggers a DomainException, otherwise the result would be undefined or become infinite. Then, a sum of the reciprocals is computed: array_map() calculates the reciprocal of each element, array_sum() sums them.
The direct formula divides the number of observations n by the obtained sum, according to the mathematical definition.

Truncated mean (or trimmed mean)

When a sample contains extreme outliers that risk distorting the arithmetic mean, an elegant solution is the truncated mean (or trimmed mean).

A percentage p% (typically 5% or 10%) is chosen, the sample is sorted, and the first k smallest and the last k largest observations are discarded, where:

\bar{x}{\text{trim}} \;=\; \frac{1}{\,n-2k\,} \sum{i=k+1}^{\,n-k} x_{(i)} .

This way, a measure of central tendency is obtained that is more robust than the arithmetic mean but less drastic than the median.

/**
 * Calculates the trimmed mean of the dataset.
 *
 * @param float $percent Percentage (0–50) of data to trim at each tail.
 * @throws \DomainException If $percent is out of range or removes all data.
 * @return float The trimmed mean.
 */
public function trimmedMean(float $percent): float
{
    if ($percent < 0.0 || $percent >= 50.0) {
        throw new \DomainException('Percent must be in the range 0 <= p < 50.');
    }

    $count = count($this->data);
    if ($count < 3) {
        // Too few values to trim meaningfully; fall back to arithmetic mean
        return $this->mean();
    }

    // Clone and sort to preserve original order
    $sorted = $this->data;
    sort($sorted, SORT_NUMERIC);

    // Number of elements to trim from each end
    $k = (int) floor($count * $percent / 100.0);

    // Ensure at least one value remains
    if ($k * 2 >= $count) {
        throw new \DomainException('Trim percentage removes all data.');
    }

    $trimmed = array_slice($sorted, $k, $count - 2 * $k);

    return array_sum($trimmed) / count($trimmed);
}

The method begins by verifying that the chosen trimming percentage makes sense: it must be greater than or equal to zero and strictly less than fifty, otherwise an exception is thrown; if, for example, we were to request the removal of 60% of the data from each tail, there would be nothing left to average.

If the sample contains fewer than three observations, the function considers trimming meaningless and simply returns the arithmetic mean: with two values, removing even one would eliminate half the data, while with only one there is nothing to trim.

The process then proceeds by cloning the original array and sorting it in ascending order; cloning preserves the order in which the data was provided to the object, while sorting is essential because trimming is applied starting from the extremes of the distribution.

The number of elements to discard at each tail, denoted by k, is obtained by multiplying the sample size by the requested percentage and rounding down; for example, if we have ten values and want a 10% trimmed mean, we will remove one element from the beginning and one from the end.

Before proceeding, the method checks that “twice k” is not equal to or greater than the length of the array: if it were, the trimming would remove all the data and the mean would no longer make sense; in such case, an additional exception is thrown.

Once this check is passed, array_slice() extracts the central portion that remains after discarding the k smallest and k largest values; the arithmetic mean is then calculated on this subset, which is precisely the desired trimmed mean.

The function thus returns a measure of central tendency that is more robust than the classic mean: the outliers, removed before the calculation, can no longer pull the result toward extreme values.

Range

The range is the simplest measure of dispersion: it indicates the total spread of the observed values, that is, the distance between the minimum and maximum extremes of the sample. If we denote

x_{\min} = \min(x_1,\dots,x_n) \quad\text{e}\quad x_{\max} = \max(x_1,\dots,x_n),

then the range R is defined as

R = x_{\max} \;-\; x_{\min}.

Although it is sensitive to outliers (the same value that affects the maximum or minimum also affects the range), this measure provides an immediate indication of the distribution’s spread and is often reported alongside the mean or median to give a quick overview of overall dispersion.

/**
 * Calculates the range (max – min) of the dataset.
 *
 * @return float The range of the data.
 */
public function range(): float
{
    // min() e max() sono O(n) ma il dataset è già in memoria: soluzione lineare
    return max($this->data) - min($this->data);
}

As can be seen, the method is very straightforward. It invokes the native PHP functions max() and min(), which each perform a single linear scan of the array to identify the largest and smallest values, respectively. Subtracting the minimum from the maximum yields the total spread of the sample; the result is returned as a float, consistent with the other methods in the class.

Quartiles and interquartile range (IQR)

To describe the dispersion of a sample more robustly than with the simple range, quartiles are used:

  • Q_1 – 25th percentile (first quartile)
  • Q_2 – 50th percentile (median)
  • Q_3 – 75th percentile (third quartile)

The interquartile range is defined as \text{IQR} = Q_3 - Q_1 and represents the spread of the central half of the data. It is not very sensitive to outliers because it is based only on the values between the 25th and 75th percentiles of the distribution.

A classic use of the IQR is outlier detection using Tukey’s method (values less than Q_1 - 1.5 \, \text{IQR} or greater than Q_3 + 1.5 \, \text{IQR}).

/**
 * Returns an array with the first, second (median) and third quartile.
 *
 * Method: "Tukey hinges".
 *  - Sort the dataset.
 *  - For Q1 and Q3, exclude the median when the sample size is odd.
 *
 * @return float[] [Q1, Q2, Q3] in ascending order.
 */
 public function quartiles(): array
    {
        $sorted = $this->data;
        sort($sorted, SORT_NUMERIC);

        $n = count($sorted);
        if ($n === 1) {
            return [$sorted[0], $sorted[0], $sorted[0]];
        }
        $mid = intdiv($n, 2);

        // Median (Q2)
        $q2 = ($n % 2 === 0)
            ? ($sorted[$mid - 1] + $sorted[$mid]) / 2.0
            : (float) $sorted[$mid];

        // Lower half (exclude median if n is odd)
        $lower = array_slice($sorted, 0, $mid);
        // Upper half (exclude median if n is odd)
        $upper = array_slice($sorted, ($n % 2 === 0) ? $mid : $mid + 1);

        // Q1 and Q3 are medians of the two halves
        $q1 = $this->medianOfArray($lower);
        $q3 = $this->medianOfArray($upper);

        return [$q1, $q2, $q3];
    }

/**
 * Calculates the interquartile range (Q3 – Q1).
 *
 * @return float The interquartile range.
 */
public function iqr(): float
{
    [$q1, , $q3] = $this->quartiles();
    return $q3 - $q1;
}

/* ---------- Helper ---------- */
/**
 * Median of a pre-sorted array (helper for quartiles).
 *
 * @param float[] $arr Sorted numeric array.
 * @return float Median value.
 */
private function medianOfArray(array $arr): float
{
    $count = count($arr);
    if ($count === 0) {
        throw new \LogicException('Cannot compute median of an empty array.');
    }

    $mid = intdiv($count, 2);

    return ($count % 2 === 0)
        ? ($arr[$mid - 1] + $arr[$mid]) / 2.0
        : (float) $arr[$mid];
}

When the quartiles() method is called, the first thing it does is create a copy of the internal data and sort it in ascending order; this copy preserves the original order provided by the user and allows working with a monotonically ordered vector, which is a necessary prerequisite for identifying quartiles. Immediately afterward, the variable $n stores the sample size, and $mid represents the central index calculated via integer division. With these two pieces of information, the median of the entire sample is determined, which becomes the second quartile Q_2; if the number of observations is even, the median is the arithmetic mean of the two central values, whereas in the odd case, it coincides with the value at the central position.

Once Q_2 is known, the sorted array is split into two halves. If the sample size is odd, the median must not be included in either the lower or upper part, so the function array_slice explicitly excludes it; if it is even, the division occurs exactly in half. At this point, the outer quartiles come into play: to calculate Q_1 and Q_3, no new object is created—rather, the private helper medianOfArray is invoked on the two already sorted halves. This small routine receives a vector, counts its elements, determines the central index, and returns the median using the same logic as before; all of this remains confined within the class, keeping the public interface clean and avoiding any code duplication.

The quartiles() method finally returns an array with the three values [Q_1, Q_2, Q_3] in ascending order. Its counterpart, iqr(), simply unpacks that array, subtracts Q_1 from Q_3, and returns the interquartile range, providing in a single call the most robust measure of dispersion in the class.

In this setup, the logic for computing the median remains centralized within the private helper, and is reused both for quartiles and, implicitly, for any other internal functionality that might need to calculate a median on a sorted subset. Meanwhile, the public API continues to offer self-explanatory and easy-to-understand methods for anyone integrating your library.

Variance

To measure how much the values deviate from their central tendency, variance is introduced, which calculates the mean of the squared deviations from the arithmetic mean. Given n observations x_1, x_2, \dots, x_n with mean \bar{x}, the population variance is defined as:

\sigma^{2} \;=\; \frac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^{2}

If instead the data represent a sample drawn from a larger population, the correct estimator (sample variance) divides by n − 1:

s^{2} \;=\; \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^{2}

Variance returns a quadratic value: it is always non-negative and increases rapidly as deviations grow. For this reason, it is often used in conjunction with its square root (standard deviation) to return to the same units of measurement as the data.

/**
 * Calculates the variance of the dataset.
 *
 * @param bool $sample If true, uses (n-1) in the denominator (sample variance).
 *                     If false, uses n (population variance).
 * @return float The variance value.
 */
public function variance(bool $sample = false): float
{
    $n = count($this->data);

    // For a single value, population variance is 0, sample variance is undefined
    if ($n < 2 && $sample) {
        throw new \DomainException('Sample variance requires at least two observations.');
    }
    if ($n === 1) {
        return 0.0;
    }

    $mean = $this->mean();
    $sumSquares = 0.0;

    foreach ($this->data as $v) {
        $diff        = $v - $mean;
        $sumSquares += $diff * $diff;
    }

    $denominator = $sample ? ($n - 1) : $n;
    return $sumSquares / $denominator;
}


The method receives a flag indicating whether to calculate the population variance or the sample estimator. It begins by evaluating the dataset size: with only one value, the population variance is by definition zero, whereas the sample variance does not exist and an exception is thrown. Once the mean is known, the loop traverses each observation, subtracts the mean, squares the deviation, and accumulates it. After the summation is complete, the division is performed by n or n − 1 depending on the specified context, thus returning the desired measure of dispersion.

Standard deviation


The standard deviation is simply the square root of the variance: it serves to bring the measure of dispersion back to the same units as the original data. If variance indicates “how many squared units” the observations deviate on average from their mean, the standard deviation expresses that deviation in linear units, making it much more intuitive for a non-specialist reader. For the population, it is obtained as \sigma = \sqrt{\sigma^{2}} while in the sample case it is s = \sqrt{s^{2}}. Small standard deviation values indicate a distribution concentrated around the mean; large values indicate widely dispersed data. 

/**
 * Calculates the standard deviation of the dataset.
 *
 * @param bool $sample If true, returns the sample standard deviation (n-1 in the denominator).
 *                     If false, returns the population standard deviation.
 * @return float The standard deviation.
 */
public function standardDeviation(bool $sample = false): float
{
    return sqrt($this->variance($sample));
}


The method contains no additional logic: it simply calls variance() with the same flag and returns its square root, delegating all calculation and domain checks to the already tested algorithm.

Standard error of the mean

When we observe only a sample from the population, the sample mean is an estimate subject to fluctuations: the smaller the sample, the more the estimate may vary from one sample to another. The standard error of the mean (SEM) precisely quantifies this expected variability. If s is the sample standard deviation and n is the sample size, the standard error is calculated as

\text{SEM} \;=\; \frac{s}{\sqrt{n}}.

A small SEM indicates that the mean calculated from that sample is likely close to the true population mean; a large SEM suggests greater uncertainty. The SEM is also the basis for constructing confidence intervals for the mean. 

/**
 * Calculates the standard error of the mean (SEM) of the dataset.
 *
 * SEM = sample standard deviation / sqrt(n)
 * Requires at least two observations.
 *
 * @throws \DomainException If the dataset size is less than 2.
 * @return float The standard error of the mean.
 */
public function standardError(): float
{
    $n = count($this->data);

    if ($n < 2) {
        throw new \DomainException('Standard error requires at least two observations.');
    }

    return $this->standardDeviation(true) / sqrt($n);
}


The method first retrieves the sample size; if there is only one value, it makes no sense to speak of standard error, so a domain exception is raised. In all other cases, it calls the already implemented sample standard deviation method to obtain s. By dividing s by the square root of n, it computes the SEM according to the canonical statistical definition and returns the result as a floating-point value. In this way, all numerical logic remains consistent with the other measures of dispersion: the function relies on well-tested methods, does not replicate existing calculations, and guarantees a very simple usage contract.

Mean absolute deviation (MAD)

To measure dispersion in an intuitive way, without amplifying deviations by squaring them as variance does, the mean absolute deviation (MAD) is used. The idea is simple: calculate the absolute distance between each observation and the arithmetic mean, then take the average of those distances. If the sample consists of the values x_1, x_2, \dots, x_n and their mean is \bar{x}, the mean absolute deviation is given by:

\text{MAD} \;=\; \frac{1}{n}\sum_{i=1}^{n} \lvert x_i - \bar{x} \rvert.

The mean absolute deviation maintains the same units of measurement as the data, is less sensitive to outliers than the standard deviation, and offers an immediate interpretation: it indicates by how many units, on average, each value deviates from the center of the distribution.

/**
 * Calculates the mean absolute deviation (MAD) of the dataset.
 *
 * @return float The mean absolute deviation.
 */
public function meanAbsoluteDeviation(): float
{
    $mean = $this->mean();
    $sumAbs = 0.0;

    foreach ($this->data as $v) {
        $sumAbs += abs($v - $mean);
    }

    return $sumAbs / count($this->data);
}


The method first retrieves the arithmetic mean of the sample using the already existing mean() function. With this information, it iterates over each observation, subtracts the mean, takes the absolute value of the deviation, and accumulates it in $sumAbs. Once the loop is complete, it divides the sum of absolute deviations by the sample size, returning the result as a floating-point number. The logic remains linear and without conditional branches because the MAD formula does not require distinctions between population and sample: division by n always applies.

Percentiles

To locate any given value along the distribution, percentiles are used: the pth percentile identifies the point below which exactly p % of the ordered data fall. The 50th percentile coincides with the median, the 25th and 75th form the quartiles already implemented, and in general, knowing multiple percentiles allows for a very detailed description of the distribution’s shape. Since the sample is finite, the percentile position rarely corresponds to an exact integer index: interpolation between adjacent elements is therefore required. A widely adopted convention (Excel and NumPy “linear” method) consists in calculating:

r = \frac{p}{100}\,(n-1)

where n is the sample size: if r falls between indices k and k+1, the percentile is the linear combination of the two values, weighted by the fractional part of r.

/**
 * Returns the p-th percentile of the dataset (linear interpolation).
 *
 * @param float $p Percentile in the closed range [0, 100].
 * @throws \DomainException If $p is outside 0–100.
 * @return float The requested percentile.
 */
public function percentile(float $p): float
{
    if ($p < 0.0 || $p > 100.0) {
        throw new \DomainException('Percentile must be between 0 and 100.');
    }

    $sorted = $this->data;
    sort($sorted, SORT_NUMERIC);
    $n = count($sorted);

    // Edge cases: 0th and 100th percentile
    if ($p === 0.0)   { return (float) $sorted[0]; }
    if ($p === 100.0) { return (float) $sorted[$n - 1]; }

    // Linear-interpolated rank
    $rank        = ($p / 100.0) * ($n - 1);
    $lowerIndex  = (int) floor($rank);
    $upperIndex  = (int) ceil($rank);
    $weightUpper = $rank - $lowerIndex;

    // If rank is an integer, no interpolation is needed
    if ($lowerIndex === $upperIndex) {
        return (float) $sorted[$lowerIndex];
    }

    $lowerValue = $sorted[$lowerIndex];
    $upperValue = $sorted[$upperIndex];

    return (1.0 - $weightUpper) * $lowerValue + $weightUpper * $upperValue;
}


The method first validates that the requested percentile lies between 0 and 100 inclusive, thus ensuring consistency with the statistical definition. It then creates a sorted copy of the data, since any percentile localization requires a monotonically increasing vector. The boundary cases 0 and 100 are handled explicitly by returning the minimum and maximum of the sample, respectively. For all other values, the real rank r is calculated, which may fall between two integer indices; the lower and upper indices define the interval containing the fractional position. If r is already an integer, no interpolation is needed and the method returns the corresponding element directly. Otherwise, the lower and upper values are linearly combined using a weight equal to the decimal part of r, yielding a continuous result that flows smoothly between the elements of the sample.

Minimum and Maximum


To complete the overview of descriptive measures, it is useful to be able to quickly retrieve the lower and upper extremes of the distribution. The minimum value indicates the smallest observation recorded in the sample; the maximum marks the largest. These two quantities, although extremely simple, are essential both for providing context to the data (knowing where the observed interval begins and ends) and as components of other statistics, such as the range you have already implemented. Since the dataset is entirely in memory, finding the minimum and maximum requires only a single linear scan, and the computational cost is negligible. 

/**
 * Returns the minimum value of the dataset.
 *
 * @return float The smallest observation.
 */
public function minValue(): float
{
    return (float) min($this->data);
}

/**
 * Returns the maximum value of the dataset.
 *
 * @return float The largest observation.
 */
public function maxValue(): float
{
    return (float) max($this->data);
}


The PHP functions min() and max() scan the array only once; the cast ensures that the returned type is float, consistent with the rest of the API.

Conclusions

With this final method, we have completed our DescriptiveStats class, which now encapsulates in a single component the most important tools of descriptive statistics: from measures of central tendency (arithmetic mean, median, mode, percentiles) to measures of dispersion (range, variance, standard deviation, IQR, MAD), including indicators of robustness (trimmed mean) and uncertainty (standard error).
Each function is self-contained, strongly typed, and supported by automated PHPUnit tests, which we have not included here so as not to further lengthen an article already rich in content.

Thanks to this library, a PHP project can quickly analyze small datasets without external dependencies and without having to use artificial intelligence just to compute a “mode”, integrate statistical calculations into reports, dashboards, or APIs, and extend the class with additional indicators by leveraging a clear and consistent architecture.

In the next article, we will see how to transform the code into a Composer package: we will create the final structure of the repository, review how to modify the composer.json file, configure CI to run the tests, and publish the library on Packagist, making it installable with a simple:

composer require thesimon82/descriptive-statistics

In this way, you will be able to distribute your open-source solution, receive contributions from the community, and reuse it in any project with maximum simplicity.

Simone Renzi
Seguimi
Latest posts by Simone Renzi (see all)

Scegli un'area

Accesso Utenti
Accesso Rete Vendita

CONTATTACI

Ti risponderemo entro 24 ore

TORNA SU